遂にこの季節がやってきた。
そう、コンビニやスーパーでアイスボックス(森永製菓)のコーナーが設置されるのである。
こんなに嬉しいことはない。
俺は1日で2つや3つ食べることがあるので、食費の10%~20%はアイスボックスが占めていることになる。それほどアイスボックスが好きな偏食だ。医学的には「氷食症」というものもあるようで、もしかしたら俺もそうなのかもしれない。
そんなことは置いといて、アイスボックスの素晴らしさを主張したい。
・うまい!!
・体の中に熱が渦巻いているようなときに食べると体温が10℃くらい下がったんじゃないかってくらい急冷される。冷房をつけた部屋で食べると寒気すら感じるほどだ。夏にピッタリ。
・そして何より、ダイエットに最適なのである。
氷をガリガリ食べるので、満足感がある。
ダイエット中でもアイスを食べたくなるときはある。そんなときに高脂質高糖質高カロリーなアイスしか並んでいないアイスコーナーのラインナップを見て泣く泣く諦めることがある。そんなとき、アイスボックスは救世主になるのだ。
なんと、13kcalと低カロリーなのである。
そして「低カロリー」という言葉で終わらせるつもりはない。
以下のように、熱力学的に考えると「0カロリー」と言えてしまうほどなのである。
-20℃に保管していたアイスボックスを我々の体に取り入れたとき、アイスボックスが我々の体から奪う熱量を概算してみる。
安易に考えると、-20℃→37℃に温度上昇していく際に吸収される熱量だけを計算してしまうが、これだけではない。氷から水へ相転移する際に、融解熱としても熱を吸収するのである。図にすると、以下のような感じだ。
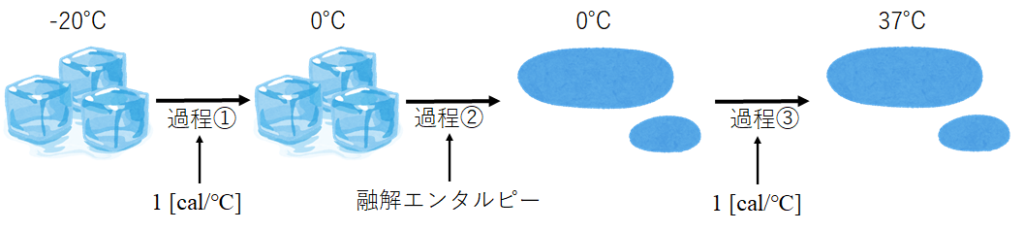
過程①は、-20℃の水が0℃になる過程である。
水1gが1℃温度上昇するのに必要な熱量は1calである。
アイスボックスは135mLなので氷135gと考えると、
135 x 20 = 2700 cal = 2.7kcalとなる。
過程②は、氷から水に相転移する過程である。
これには融解エンタルピーというものが必要とされる。
ググってみると氷(18 g/mol)の融解エンタルピーは6.01 kJ/molらしい。
アイスボックス、即ち氷135 gは、
135g ÷ 18g/mol =7.5 mol。
アイスボックスが液体になるのに必要な熱量は、
6.01 kJ/mol x 7.5 mol = 45.075 kJである。
1calは、4.184Jなので、単位変換すると
45.075 kJ = 10.773 kcalである。
過程③は、0℃の水が37℃(ヒトの体温)になる過程である。
過程①と同じく、水1gが1℃温度上昇するのに必要な熱量は1calである。
アイスボックスは135mLなので氷135gと考えると、
135 x 37 = 4995 cal = 4.995 kcalとなる。
3過程を合計すると、
2.7 kcal + 10.773 kcal + 4.995 kcal ≒ 18.5 kcalとなる。
なんということだ。アイスボックスのカロリー13kcalを超える熱量が必要とされるということだ。つまり、食べれば食べるほど痩せていくのだ(?)。
こう書くと、アイスボックスだけを食べて生活するような人がでてくるので、先に言っておくが、体を壊すだけなので止めてください。ダイエットは長期的・計画的に。
とはいえ、アイスボックスはダイエッターに適したアイスと言えるだろう。
ただし、ダイエットにつながるからといって、買い占めるような真似はしないでいただきたい。俺が買えなくなっちゃうので。
大昔に勉強した熱力学の知識がこんなところで活きてくるとは思わなかった。
そして、水1gを1℃上げるのに必要な熱量と比べて、氷→水への状態変化にこれだけ大きな熱量が必要なことは改めて驚きである。
水の融解熱は、氷として静止している水分子を、振動させて液体としての流動性を持たせるために必要な熱量と解釈することができる。確かに、これをイメージすると、なんとなく氷(-20℃)→氷(0℃)、水(0℃)→水(37℃)の温度上昇に必要な熱量よりも水分子が動き出すために必要な熱量の方が大きそうに感じる。
※計算に関して、間違いがあればご指摘ください。

コメント